T-PROGS

Why T-PROGS with GMS?
GMS provides a custom interface to the T-PROGS utility offering a simple way to set model parameters and a graphical user interface to run the model and visualize the results. Gather background data from a variety of sources from GIS to CAD and access online data from numerous databases of maps, images, and elevation data. GMS allows you to interact with models in true 3D taking advantage of optimized OpenGL graphics and to create photo-realistic renderings and animations for PowerPoint, print, and web presentations.

Try GMS Free for 14 Days   >Purchase GMS with T-PROGS   >

T-PROGS Description:
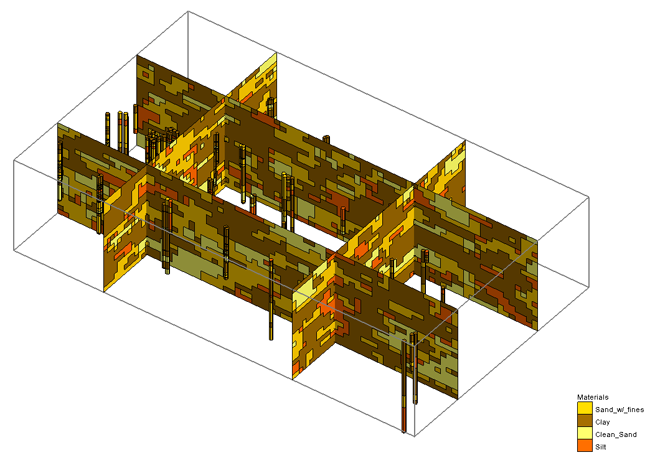
The T-PROGS software is used to perform transition probability geostatistics on borehole data. The output of the T-PROGS software is a set of N material sets on a 3D grid. Each of the material sets is conditioned to the borehole data and the materials proportions and transitions between the boreholes follows the trends observed in the borehole data. These material sets can be used for stochastic simulations with MODFLOW. A sample material set generated by the TPROGS software is shown below. The T-PROGS software can also be used to generate multiple input data sets for the HUF package.

The T-PROGS software utilizes a transition probability-based geostatistical approach to model spatial variability by 3-D Markov Chains, set up indicator cokriging equations , and formulate the objective function for simulated annealing. The transition probability approach has several advantages over traditional indicator kriging methods. First, the transition probability approach considers asymmetric juxtapositional tendencies, such as fining-upwards sequences. Second, the transition probability approach has a conceptual framework for incorporating geologic interpretations into the development of cross-correlated spatial variability. Furthermore, the transition probability approach does not exclusively rely on empirical curve fitting to develop the indicator (cross-) variogram model. This is advantageous because geologic data are typically only adequate to develop a model of spatial variability in the vertical direction. The transition probability approach provides a conceptual framework to geologic insight into a simple and compact mathematical model, the Markov chain. This is accomplished by linking fundamental observable attributes – mean lengths, material proportions, anisotropy, and juxtapositioning – with Markov chain model parameters.