National Flood Frequency (NFF)
The USGS in cooperation with the FHWA and FEMA have developed state by state regression equations that can be used to predict peak runoff of ungaged watersheds from the historical records and regression analysis of "hydrologically" similar gaged watersheds. Hydrologic similarity generally means within the same climate, elevation, and and use region. Each state is divided into similar regions like the ones shown for Colorado below. Within these regions several gages where historical flows have been measured (black points in the Colorado map) are used to develop regression equations based on characteristic watershed and meteorological variables. When a peak flow estimate is desired for an ungaged drainage, the regression equation is used for the region where the ungaged basin is located.
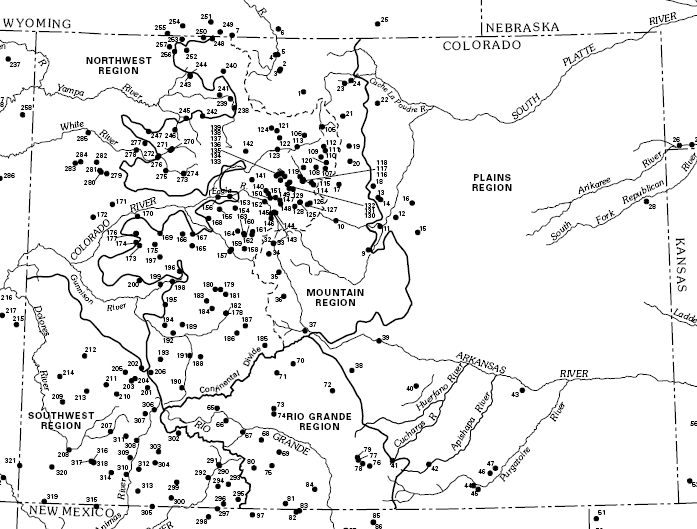
For example the Colorado equations for the 100 year flood for the different regions are as follows:
Mountain
Q100 = 39.5(A)0.706(S+1.0)1.577
Where A = area, S = slope
Rio Grande
Q100 = 1.19(A)0.846(P)1.074 Where A = area, P = precipitation
Southwest
Q100 = 118.4(A)0.715 Where A = area
Northwest
Q100 = 104.7(A)0.624 Where A = area
Plains Region
Q100 = 1640(A)0.388
Where A = area
It should come as no surprise that all of the equations contain Area as an indicator variable. While the Mountain equation uses a measure of watershed slope, the Rio Grande uses the mean annual precipitation.
Each state has been similarly divided and using historical information, regression equations for the 2, 5, 10, 25, 50, 100, and in some cases 500 year events have been defined. Two strengths of the regression equations are: 1) the ability to quickly estimate peak flows from variables typically determined for a watershed study; and 2) They do not rely on converting rainfall to runoff through numerical methods. The disadvantage is that while equations have been defined for each state, there is still significant uncertainty in results because of inadequate information. For this reason regression equations should be used cautiously, and where applicable, compared with results from a deterministic model.

